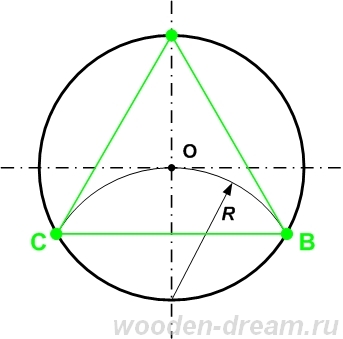
Окружность можно поделить на три части, если, используя циркуль, из точки пересечения прямой, проведенной через центр окружности O, сделать циркулем засечки B и C на линии окружности величиной, равной радиусу этой окружности. Таким образом, будут найдены две искомые точки, а третья – это противоположная точка A, где пересекаются окружность и прямая. Далее, если это необходимо, при помощи линейки и карандаша можно вычертить встроенный треугольник.
Разделить окружность небольшого диаметра на четыре части можно просто проведя две прямые NS и MP через центр окружности O под углом в 90° (прямой угол). Точки пересечения диаметров и окружности и будут искомыми точками (M,N,P,S). Чтобы разделить на четыре части окружность большого диаметра необходимо воспользоваться линейкой и циркулем. Для построения перпендикулярного диаметра нужно из точки пересечения с окружностью первого диаметра, провести циркулем дугу, несколько большей величины, чем радиус этой окружности. А затем провести вторую дугу из противоположной точки пересечения диаметра и окружности. Через точки пересечения этих дуг и будет проходить перпендикулярный первому диаметр. Подобным образом можно делить отрезки пополам .
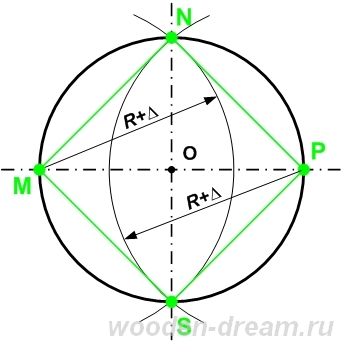
- Соответственно, для разделения окружности на восемь частей необходимо построить две пары таких диаметров.
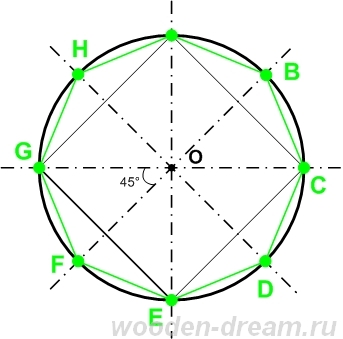
- Для того чтобы разделить окружность ровно на пять частей, можно воспользоваться двумя способами.
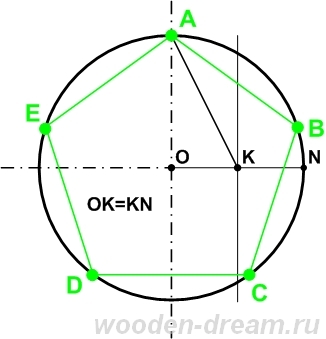
- Можно разделить окружность при помощи транспортира на пять равных частей. Простым вычислением получаем 360°/5 =72°. Это значит, каждый следующий центральный угол в 72° будет отделять пятую часть окружности. После соединения всех точек деления окружности можно получить вписанный правильный пятиугольник.
- На линии диаметра находится точка K, разделяющая отрезок радиуса пополам. Из K проводится прямая линия через точку пересечения перпендикулярного диаметра и окружности. Из точки K чертится отрезок AK, который и равен 1/3 окружности. Данный отрезок замеряется циркулем и последовательно откладывается на окружности.
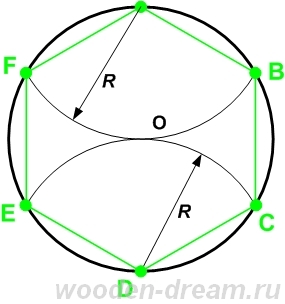
 Для того чтобы разделить окружность ровно на шесть частей, необходимо провести две дуги радиуса окружности из точек пересечения диаметра и окружности A и D. При соединении хордами полученных точек B,F и C,E, получается правильный вписанный шестиугольник, причем, его вершины находятся в точках разделения окружности на шесть частей.
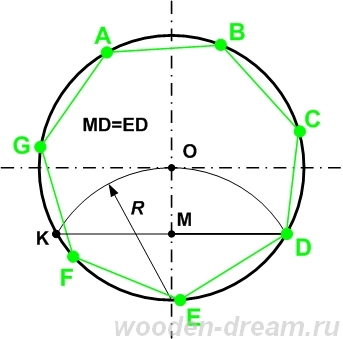
 - При делении окружности на семь одинаковых частей из точки ее пересечения с вертикальным диаметром нужно провести вспомогательную дугу величиной, равной радиусу R. Точки K и D, где она пересекается с окружностью, образуют хорду, равную стороне вписанного в нее треугольника. Половина этого отрезка будет примерно равна стороне вписанного семиугольника, значит, разделит окружность на семь частей.
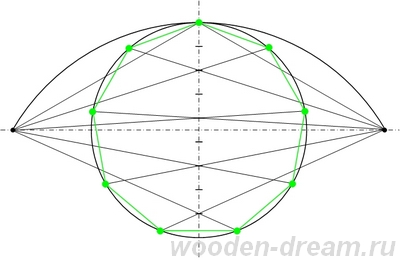
 - Теперь, чтобы разделить любую окружность на большее количество одинаковых частей (n частей), например на девять, нужно прочертить два перпендикулярных друг другу диаметра. Затем один из них разделить на 9 равных частей. Из точки пересечения этого диаметра и окружности провести дугу, величиной, равной диаметру этой окружности, до точек пересечения ее со вторым диаметром. Теперь, если из этих точек провести лучи, проходящие через нечетные или четные точки деления первого диаметра в окружности, то можно, с небольшой погрешностью, получить точки деления окружности на нужное количество равных частей. Погрешность сравнительно мала и составляет примерно 0,01R. Что на практике не играет существенной роли.
 - Всем спасибо за прочтение данной полезной статьи.
|